Modelling porous medium modification Induced Calcite Precipitation
SFB Project Area C: Biomineralization
What is Induced Calcite Precipitation (ICP)?
Microbes change the chemistry in a way that promotes the precipitation of calcite.
What is ICP?
 Credit: James
Connolly, Montana State University.
Credit: James
Connolly, Montana State University.
Results of ICP
Segmented CT image of a glass-bead column mineralized by ICP


Credit: Johannes Hommel, University of Stuttgart
Why investigate ICP?
 Mineralized
sand, photo by Johannes Hommel, University of Stuttgart.
Mineralized
sand, photo by Johannes Hommel, University of Stuttgart.
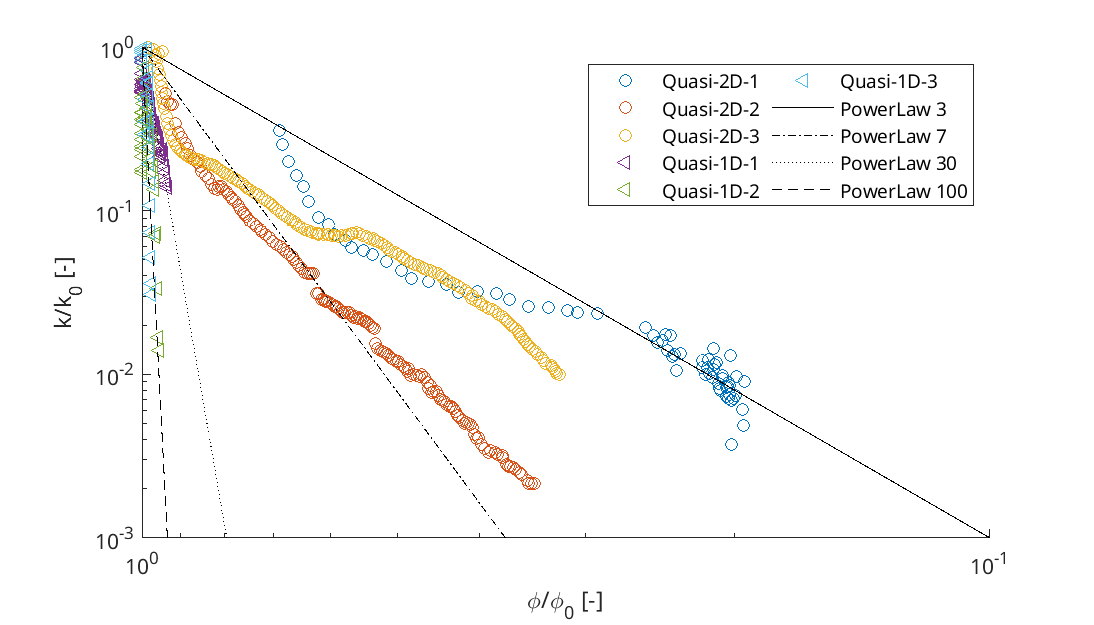 Porosity-Permeability changes observed by Felix Weinhardt,
University of Stuttgart.
Porosity-Permeability changes observed by Felix Weinhardt,
University of Stuttgart.
Why investigate ICP?
Applications in which a porous medium should be cemented in-situ, e.g. sealing, leakage mitigation, creating subsurface barries, reducing erosion, or stabilizing soil.
Main desired effects of ICP in those applications are:
- reduce flow (reduce \(K\) and \(k_r\), increase \(p_c\))
- increase mechanical strength
Model concept
Model concept: Relevant processes
 (modified after Ebigbo et
al., WRR 2012)
(modified after Ebigbo et
al., WRR 2012)
- Two-phase transport
Model concept: Relevant processes
 (modified after Ebigbo
et al., WRR 2012)
(modified after Ebigbo
et al., WRR 2012)
- Two-phase, multi-component transport
Model concept: Relevant processes
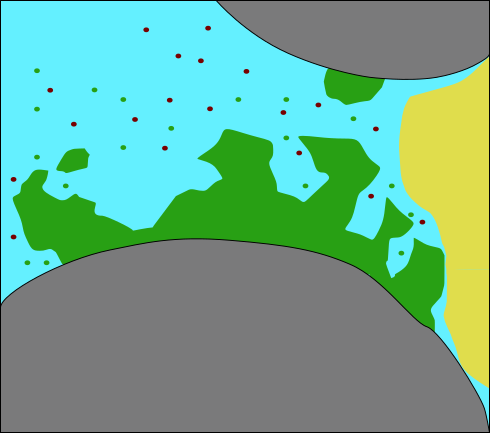 (modified after
Ebigbo et al., WRR 2012)
(modified after
Ebigbo et al., WRR 2012)
For this exercise: Neglecting microbial growth and decay, attachment and detachment
- Biomass (S. pasteurii)
- growth / decay
- attachment / detachment
Model concept: Relevant processes
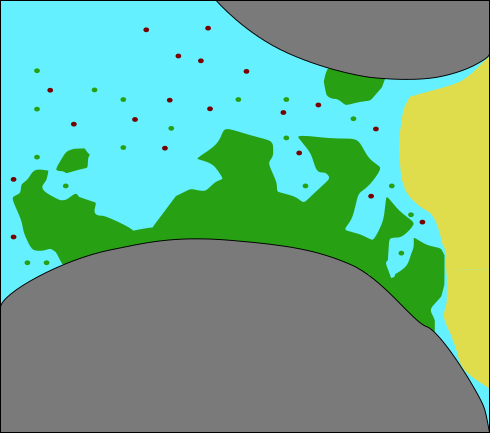 (modified after Ebigbo
et al., WRR 2012)
(modified after Ebigbo
et al., WRR 2012)
- Urea hydrolysis \[ \begin{aligned} \underset{\text{urea}}{\mathrm{CO(NH_2)_2}} + 2 \mathrm{H_2O} \overset{\text{urease}}{\rightarrow} \\ \underset{\text{ammonia}}{\mathrm{2NH_3}} + \underset{\text{carbonic acid}}{\mathrm{H_2CO_3}} \end{aligned} \]
MICP: Main reactions
Here: Ureolytic microbes produce the enzyme urease (MICP) \[ \mathrm{CO(NH_2)_2 + 2 H_2O + Ca^{2+} \rightarrow 2 NH_4^+ + CaCO_3} \]
Different reactions in detail:
\[ \begin{array}{lr} \mathrm{CO(NH_2)_2 + 2 H_2O \rightarrow 2 NH_3 + H_2CO_3} \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! & \text{ureolysis} \\ \mathrm{H_2CO_3 \rightleftharpoons HCO_3^- + H^+} & \text{dissociation of carbonic acid} \\ \mathrm{HCO_3^- \rightleftharpoons CO_3^{2-} + H^+} & \text{dissociation of bicarbonate ion} \\ \mathrm{2 NH_4^+ \rightleftharpoons 2 NH_3 + 2 H^+} & \text{dissociation of ammonia} \\ \mathrm{Ca^{2+} + CO_3^{2-} \rightleftharpoons CaCO_3 \downarrow} & \text{calcite precipitation/dissolution} \end{array} \]
Model concept: Relevant processes
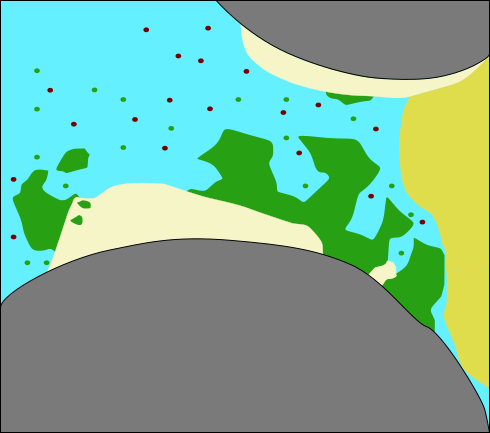 (modified
after Ebigbo et al., WRR 2012)
(modified
after Ebigbo et al., WRR 2012)
- Precipitation and dissolution of calcite
\[ \mathrm{ \underset{\text{calcium}}{Ca^{2+}} + \underset{\text{carbonate}}{CO_3^{2-}} \rightleftharpoons \underset{\text{calcite}}{CaCO_3 \downarrow} } \]
Model concept: Relevant processes
 (modified after
Ebigbo et al., WRR 2012)
(modified after
Ebigbo et al., WRR 2012)
Clogging: Reduction of porosity \[ \phi = \phi_0 - \phi_\text{biofilm} - \phi_\text{calcite} \]
and reduction in permeability: Kozeny-Carman relation \[ K = K_0 \left( \frac{1-\phi_0}{1-\phi} \right)^2 \left( \frac{\phi}{\phi_0} \right)^3 \] or the Power Law
Equations
Balance Equations
Mass balance equation of components \[ \Sigma_\alpha \frac{\partial}{\partial t}(\phi \rho_\alpha x^\kappa_\alpha S_\alpha)+ \nabla \cdot ( \rho_\alpha x^\kappa_\alpha \mathbf{v}_\alpha )- \nabla \cdot ( \rho_\alpha \mathbf{D}^\kappa_{\alpha;\text{pm}} \nabla x^\kappa_\alpha )= q^\kappa \]
Mass balance for the immobile components / solid phases: \[ \frac{\partial}{\partial t}(\rho_\varphi \phi_\varphi) = q^\varphi \]
Overall procedure of implementing chemical reactions in DuMu\(^\mathsf{x}\):
- Chemical equation calculate equilibrium/kinetic reaction rate e.g. \(r_\text{urea}\)
- Reaction rate set component source/sink term e.g. \(q^\varphi\) depending on and chemical reaction
Sources & Sinks:
For this exercise:
- Neglecting microbial growth and decay, attachment and detachment as we assume a fixed biofilm for simplicity!
- We also assume that the rate of precipitation is equal to the rate of ureolysis, saving the work of detailed geochemistry calculations for the sake of both simplicity and faster run times.
Sources & Sinks:
\[ \begin{aligned} &\text{Urea:} & q^{\text{urea}} &= -r_\text{urea} \\ &\text{Calcium:} & q^{\mathrm{Ca}^2+} &= -r_\text{precip} \\ &\text{Total carbon:}& q^{\mathrm{C}_\text{tot}^+} &= r_\text{urea} - r_\text{precip} \\ &\text{Calcite:} & q^{\mathrm{C}} &= r_\text{precip} \end{aligned} \]
Sources & Sinks:
\[ \begin{aligned} \qquad\qquad & \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \text{Precipitation rate:} \\ r_\text{precip} &= f\; \left( A_\text{interface}, \Omega = \frac{\left[\mathrm{Ca}^{2+}\right]\left[\mathrm{CO_3}^{2-}\right]}{K_\text{sp}}, T \right) \\ \qquad\qquad & \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \text{For this exercise:} \\ r_\text{precip} &= r_\text{urea} \\ \qquad\qquad & \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \!\!\!\!\!\! \text{Ureolysis rate:} \\ r_\text{urea} &= k_\mathrm{urease}^\mathrm{m} k_{\mathrm{urease}, \text{biofilm}} \left(\rho_\text{biofilm} \phi_\text{biofilm}\right) \frac{m_\text{urea}}{K_\text{urea} + m_\text{urea}} \end{aligned} \]
Supplementary Equation:
- Updating porosity and permeability
\[ \begin{aligned} \phi &= \phi_0 - \Sigma_\varphi \phi_\varphi \\ K &= K_0 \left(\frac{1-\phi_0}{1-\phi}\right)^2 \left(\frac{\phi}{\phi_0}\right)^3 \\ \text{or}& \\ K &= K_0 \left( \frac{\phi}{\phi_0} \right)^\eta \end{aligned} \]
Specific Implementations
- Update porosity in dumux/material/fluidmatrixinteractions/porosityprecipitation.hh
…
auto priVars = evalSolution(element, element.geometry(),
elemSol, scv.center());
Scalar sumPrecipitates = 0.0;
for (int solidPhaseIdx = 0; solidPhaseIdx < numSolidPhases; ++solidPhaseIdx)
sumPrecipitates += priVars[numComp + solidPhaseIdx];
using std::max;
return max(minPoro, refPoro - sumPrecipitates);
…Specific Implementations
- Update permeability in /material/fluidmatrixinteractions/permeabilitykozenycarman.hh
Biomineralization exercise
Exercise
- 2 aquifers with sealing aquitard
- Upper aquifer: “drinking water”
- Lower aquifer: “\(\mathrm{CO_2}\) storage”
- Problem:
- Leakage pathway
- Stored \(\mathrm{CO_2}\) would migrate to drinking water aquifer!
- Biomineralization to “seal” the leakage

Exercise tasks
- Get familiar with the code
- Implement the simplified chemical reactions
- Use source()-function to link chemistry-file to problem
- Vary parameters, so that leakage pathway is “sealed” (porosity \(<\) 0.07)
- Implement new boundary condition for \(\mathrm{CO_2}\)-injection in lower aquifer
- Exchange the permeability law from Kozeny-Carman to a Power Law
- Use tabulated values for \(\mathrm{CO_2}\)
Exercise
First step: Go to the Biomineralization Exercise and check out the README