What is a DuMu^x model

A DuMu^x model is an implementation of a discretized mathematical model, generally given by partial differential equations.

What is a DuMu^x model

Mathematical model (PDE): \[ \begin{aligned} \frac{\partial S(u)}{\partial t} + \nabla \cdot \mathbf{F}(u) = q(u), \quad \forall (t,\mathbf{x}) \in (0,T] \times \Omega \end{aligned} \]

What is a DuMu^x model

Discrete model using finite volumes: \[ \begin{aligned} \small |B| \frac{S_B(\mathbf{u}^{n+1}_h) - S_B(\mathbf{u}^{n}_h)}{\Delta t} + \sum_{\sigma \in \Sigma_B} F_{B,\sigma}(\mathbf{u}^{n+1}_h) = |B| q_B(\mathbf{u}^{n+1}_h), \quad \forall t_{n+1}\leq T, \; \forall B \end{aligned} \]

• \(B:\) control volume
• \(S_B:\) storage term
• \(F_{B,\sigma}:\) flux term over sub control volume face (scvf)
• \(q_B:\) source term

Where to implement these terms in DuMu^x?

LocalResidual

LocalResidual

Implements terms of a PDE in the functions

• computeStorage(...)
• computeFlux(...)
• computeSource(...)

Example: Diffusion equation

Mathematical model (PDE):

\[ \begin{aligned} \frac{\partial c}{\partial t} - \nabla \cdot (D \nabla c) = 0 \:\: \mathrm{in}\; \Omega \times (0,T] \end{aligned} \]

with

• \(c:\) concentration
• \(D:\) constant diffusion coefficient
• \(\Omega:\) spatial domain
• \(T:\) end time

Example: Diffusion equation

Discrete model using the Box discretization:

\[ \begin{aligned} \vert B \vert \frac{c_B^{n+1}-c_B^{n}}{\Delta t} - \sum_{\sigma \in \Sigma_{B}} \vert \sigma \vert \left[ D \nabla c_h^{n+1} \cdot \boldsymbol{n}_{B,\sigma} \right] = 0, \end{aligned} \]

Example: Diffusion equation

Discrete model using the Box discretization:

\[ \begin{aligned} \vert B \vert \frac{c_B^{n+1}-c_B^{n}}{\Delta t} - \sum_{\sigma \in \Sigma_{B}} \vert \sigma \vert \left[ D \nabla c_h^{n+1} \cdot \boldsymbol{n}_{B,\sigma} \right] = 0, \end{aligned} \]

with

• \(c_B^n:\) concentration at time \(t_n\) and control volume \(B\)
• \(c^n_h:\) global discrete solution at time \(t_n\), interpolated using basis functions
• \(\mathbf{n}:\) unit outer normal vector
• \(\sigma:\) sub control volume face (scvf)

LocalResidual

The local residual of the diffusion model:

template<class TypeTag>
class DiffusionModelLocalResidual
: public DiscretizationDefaultLocalOperator<TypeTag>
{
    ...
}

File: dumux/examples/diffusion/model.hh

Inherits from the DiscretizationDefaultLocalOperator, which is chosen depending on the discretization scheme, here Box scheme.

Storage term

NumEqVector computeStorage(const Problem& problem,
                           const SubControlVolume& scv,
                           const VolumeVariables& volVars) const
 {
    NumEqVector storage;
    storage[Indices::massBalanceEqIdx]
        = volVars.priVar(Indices::concentrationIdx);
    return storage;
 }

File: dumux/examples/diffusion/model.hh

Flux term

\[ \begin{aligned} F_{B,\sigma} = - \vert \sigma \vert D \nabla c_h^{n+1} \cdot \boldsymbol{n}_{B,\sigma} \end{aligned} \]

with

• \(c^n_h:\) global discrete solution at time \(t_n\), interpolated using basis functions
• \(\mathbf{n}:\) unit outer normal vector
• \(\sigma:\) sub control volume face (scvf)

Flux term

NumEqVector computeFlux(const Problem& problem,
                        const Element& element,
                        const FVElementGeometry& fvGeometry,
                        const ElementVolumeVariables& elemVolVars,
                        const SubControlVolumeFace& scvf,
                        const ElementFluxVariablesCache& elemFluxVarsCache) const
{
    ...
}

File: dumux/examples/diffusion/model.hh

Flux term

NumEqVector computeFlux(...) const
{
    // Compute ∇c
    const auto& fluxVarCache = elemFluxVarsCache[scvf];
    Dune::FieldVector<Scalar, dimWorld> gradConcentration(0.0);
    for (const auto& scv : scvs(fvGeometry))
    {
        const auto& volVars = elemVolVars[scv];
        gradConcentration.axpy(
            volVars.priVar(Indices::concentrationIdx),
            fluxVarCache.gradN(scv.indexInElement())
        );
    }
    ...
}

File: dumux/examples/diffusion/model.hh

Flux term

NumEqVector computeFlux(...) const
{
    ...
    NumEqVector flux;

    // Compute the flux
    flux[Indices::massBalanceEqIdx] = -1.0*scvf.area()*vtmv(
        scvf.unitOuterNormal(),
        problem.diffusionCoefficient(),
        gradConcentration
    );

    return flux;
}

File: dumux/examples/diffusion/model.hh

LocalResidual

A LocalResidual implements the discretized mathematical model.

For its implementation different model-specific properties have to be set

Model properties

All properties are defined within the namespace Dumux::Properties.

namespace Dumux::Properties {
    //define all properties
} // end namespace Dumux::Properties

File: dumux/examples/diffusion/model.hh

Model type tag

The property type tag is an empty struct with the respective name, e.g. DiffusionModel. All properties related to the desired model can be attributed using the property type tag.

namespace Dumux::Properties::TTag {
//! The diffusion model tag that we can specialize properties for
struct DiffusionModel {};
} // end namespace Dumux::Properties::TTag

File: dumux/examples/diffusion/model.hh

Defining model properties

The type of the local residual is the class DiffusionModelLocalResidual defined from earlier

template<class TypeTag>
struct LocalResidual<TypeTag, TTag::DiffusionModel>
{ using type = DiffusionModelLocalResidual<TypeTag>; };

File: dumux/examples/diffusion/model.hh

Defining model properties

The model traits specify information about the model:

template<class TypeTag>
struct ModelTraits<TypeTag, TTag::DiffusionModel>
{
    struct type
    {
        struct Indices
        {
            static constexpr int concentrationIdx = 0;
            static constexpr int massBalanceEqIdx = 0;
        };
        static constexpr int numEq() { return 1; }
    };
};

File: dumux/examples/diffusion/model.hh

Defining model properties

Further model specific properties can be set accordingly by using the model property tag, i.e. TTag::DiffusionModel

Exercise: Model

Implementation of a nonlinear diffusion model for denoising of an MRI image

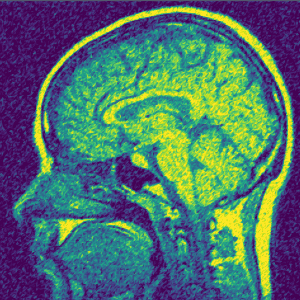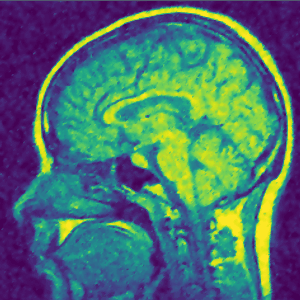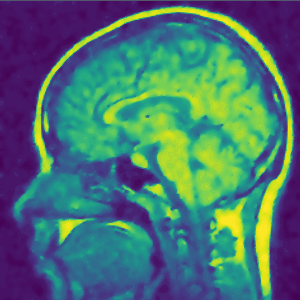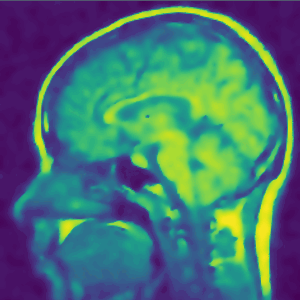
Tasks

• Implement local residual

• Set model properties

• Use model in test case

• Customize volume variables

• Go to Model exercise